 |
| http://i.cdn.turner.com/v5cache/CARTOON/site/Images/i70/adventure-time.png |
Last year, this little guy here sent me on a journey:
 |
| https://www.youtube.com/watch?v=Lt9mjoaO2oc |
As a birthday gift, my wife offered to make me a stuffed version:
 |
| I am so happy! |
There was one condition: I needed to determine what fabric pattern cut so that the bee would come out as nice as possible.
The tradition in question was these Christmas ornaments made from foam balls upholstered with petals of fabric; in my family we called them "tannenbaums" (though after a brief bit of Googling this might be something my brother made up).
 |
| https://craftsncoffee.files.wordpress.com/2014/11/diy-fabric-ornaments.jpg?w=640 |
It took some thought, but I figured the best shape of petal would be the spaced enclosed by two out-of-phase sine waves:
 |
| Made using Microsoft Math 4.0: http://www.microsoft.com/en-us/download/details.aspx?id=15702 |
Understanding this, I figured it couldn't be that much harder to figure out what "petal shape" would make a prolate spheroid. Wow, was I in for a surprise...
Looking at the drawing, I estimated the aspect ratio of the bee to be 1.25, meaning the bee was 1.25 times longer on one axis than it was on the other two. My first thought was just to stretch the petal shape along the horizontal direction, but immediately it was clear this wouldn't work. Since the overall shape needs to be perfectly round at the tips, the angle of each petal still needs to be the same: 360° divided by however many petals I decide to use. If I stretch the petal in the horizontal direction, this would change the angle at the ends of the petals. This would turn the ball not into a prolate spheroid, but a football.
I was not about to let my bee have the shape of a football! I'd have to find the shape of some weird curve I'd not heard of before. Hmm...
Imagine being small and standing on the surface of a proloate spheroid, marching from the equator to the north pole. The horizontal coordinate of our curve (u) should be how far we've traveled along the surface of the prolate spheroid. The vertical coordinate of our curve (v) should be a twelfth (since we're using six petals, and a petal is twice as tall as the curve we're looking for) of the circumference of the circle of latitude where you're at. Think of the cross section produced when slicing a lemon; you get circles. That's the circumference we're talking about.
I was pretty sure I'd end up using the formula for arc length.
 |
| http://tutorial.math.lamar.edu/Classes/CalcII/ArcLength.aspx |
Now I just needed to plug in the equation for an ellipse:
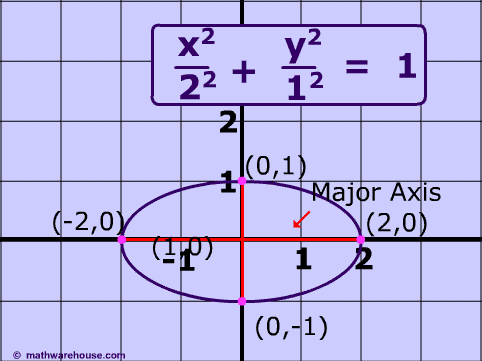 |
| http://www.mathwarehouse.com/ellipse/equation-of-ellipse.php |
Basically, it leads to a really mean integral. I cheated by looking at the answer, and I still have no idea what happened. Most students leave public school knowing the formula for a circle's circumference: C=2πr. Now, try to think back if you've ever heard the formula for an ellipse's circumference. I can almost guarantee nobody has ever even mentioned it, and here's why:
![C = 2\pi a \left[1 - \sum_{n=1}^\infty \left(\frac{(2n - 1)!!}{2^n n!}\right)^2 \frac{e^{2n}}{2n - 1}\right],](http://upload.wikimedia.org/math/0/a/1/0a1f9b3824382486507885622ddcf283.png) |
| http://en.wikipedia.org/wiki/Ellipse#Circumference |
Never-mind that this is the formula for just the circumference and I need pieces of this. I'm not even sure what coordinate system to use! Screw this. Bye bye. I need to start over.
When in doubt, solve the problem numerically
Lets define the spheroid as having semi-axes lengths of rx=1.00, ry=1.00, and rz=1.25 (these are kind of like radii). Now we just need to numerically determine u(z) and v(z) and plot the curve of v vs. u. to form the petal pattern which my wife will use to make the bee.
It'll be convenient to define r(z). This is the radius of the cross section of each slice along the z axis. Since the side view of the prolate spheroid is also an ellipse, we can use the following equation:
It'll be convenient to define r(z). This is the radius of the cross section of each slice along the z axis. Since the side view of the prolate spheroid is also an ellipse, we can use the following equation:
| Made using the equation editor in Power Point. |
Determining u(z) is harder. First we have to define n=100 or so points so that z0=0 and zn=1.25 . We then use the Pythagorean Theorem to figure out the distances between each (ri, zi) and (ri+1, zi+1), and cumulatively add everything together:
We get the following curves:
 |
| r(z) vs. z and v(z) vs. u(z) |
Now it's a simple manner of making a printout my wife can use:
 |
| Yaaaay! It's done. |
So... that was interesting or as Finn would say:
 |
| http://media.giphy.com/media/9lMoyThpKynde/giphy.gif |
.jpg)

I see your blog regularly. Your blog is very useful for us. If you are screaming out “solution” you’ve come to the most elite solution...Click Here
ReplyDelete